Das "Buddhabrot" stellt eine besondere Abbildung einer Menge der komplexen Zahlen dar und ist sehr eng mit der Mandelbrot-Menge verwandt.
Den passenden Namen erhielt die Abbildung aufgrund der Ähnlichkeit zum meditierenden Buddha, welche augenfällig wird, wenn man das Fraktal um 90° dreht:


Mandelbrotmenge
Die Mandelbrot-Menge ist die Menge aller Punkte "c" der komplexen Zahleneben, für welche die rekursiv definierte Folge
mit z0 = 0 beschränkt bleibt, also nicht gegen unendlich divergiert.
Buddhabrot
Das Buddhabrot wird - im folgenden vereinfachend dargestellt - durch eine Dichteverteilung beschrieben, die wie folgt berechnet wird:
Zuerst werden die Punkte der komplexen Zahlenbene berechnet, welche nach einer festgelegte maximalen Anzahl an Iterationen (Bailout) gegen unendlich divergieren, also nicht zur
Mandelbrotmenge gehören.
Diese werden daraufhin in einem zweiten Schritt erneut in die Mandelbrotfunktion eingesetzt. Dadurch werden diejenigen Bereiche hervorgehoben, in denen diese Werte die meiste Zeit auf dem Weg in die Unendlichkeit verbringen.
Zusammenhang zwischen Mandelbrotmenge und dem Bifurkationsdiagramm der logistischen Gleichung
Die Mandelbrotmenge und die logistische Gleichung λx (1-x) stehen durch die folgende quadratische Transformation im Zusammenhang:
Budhabrot & Anti-Buddhabrot



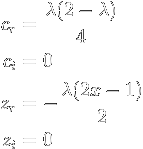
Kommentar schreiben