Koch-Kurve
Die Koch-Kurve wurde nach seinem Entdecker, dem schwedischen Mathematiker Helge von Koch (1870-1924), benannt.
Sie ist ein Beispiel für ein mathematisches Monster. Um die Jahrhundertwende zum 20. Jahrhundert wurden diese Kurven deshalb als mathematische Monster bezeichnet, weil sie nicht mit den
Vorstellungen euklidischer geometrischer Objekte in Einklang zu bringen waren. Es sind überall stetige, aber an keiner Stelle differenzierbare Kurven.
Die 1904 entdeckte Koch-Kurve gilt als eines der ersten formal beschriebenen Fraktale. Der Terminus "Fraktal" existierte zu dieser Zeit jedoch noch nicht und wurde erst Jahrzehnte später von Benoit Mandelbrot eingeführt.
Iteration der Koch-Kurve

Die Koch-Kurve ist ein streng selbstähnliches Fraktal und wird durch folgende Iteration beschrieben:
Es sei eine Strecke mit definierter Länge gegeben.
Diese Strecke wird als Initiator bezeichnet.
Im ersten Iterationsschritt entfernt man das mittlere Drittel der Strecke und ersetzt diese durch zwei Strecken, die in einem Winkel von 60° zueinander, sowie zum Initiator stehen.
Es wird also auf dem mittleren, entfernten Streckenabschnitt, ein gleichseitiges Dreieck mit der Länge der entfernten Strecke errichtet.
Dies wird als Generator bezeichnet.
Die nun vorhandenen 4 Streckenabschnitte haben jeweils eine Länge von ⅓ der Länge des Initiators.
Im folgenden Iterationsschritt wird der Generator auf jeden der 4 Streckenabschnitte angewendet.
Diese Iteration wird nun beliebig oft wiederholt und die Koch-Kurve wird mit jedem Schritt genauer abgebildet.
Konstruktion mittels Lindenmayer System
Eine alternative Konstruktion kann mittles des Lindenmayer Systems erfolgen.
Als Start wird "F" und als Ersetzungsregel "F → F + F - - F + F" definiert.
Hierbei bedeuten die Symbole folgendes:
F : Einen Strich mit definierter Länge zeichnen
+: mathematisch positive Drehung um einen bestimmten Winkel (60°)
- : mathematisch negative Drehung um einen bestimmten Winkel (60°)
Zu Beginn ist eine Strecke mit definierter Länge gegeben.
Die Kurve besteht also aus einem einzigen Streckenstück.
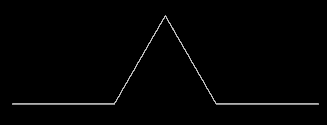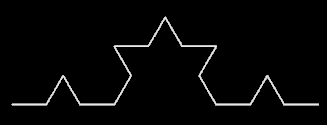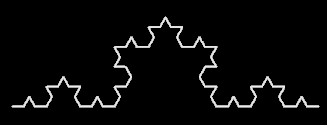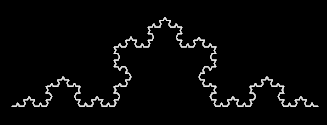
Im ersten Schritt wird dieser Streckenabschnitt durch 4 gleich lange Strecken ersetzt.
Die neue Streecke ist dabei wie folgt aufgebaut:
- erster Streckenabschnitt
- zweiter Streckenabschnitt mit Drehung um 60° (mathematisch positiv, gegen Uhrzeigersinn)
- dritter Streckenabschnitt mit Drehung um 2 x 60° = 120° (mathematisch negativ, im Uhrzeigersinn)
- vierter Streckenabschnit mit Drehung um 60° (mathematisch positiv, gegen Uhrzeigersinn)
Jeder der 4 neuen Streckenabschnitte hat ⅓ der Länge des ursprünglichen Streckenabschnitts.
Im nächsten Schritt wird jeder der 4 Streckenabschnitte durch einen Streckenabschnitt der oberen Art ersetzt.
Für n gegen Unendlich geht die Anzahl der Streckenabschnitte gegen Unendlich.
Mit n= Anzahl der Iterationen ist die die Länge der Gesamtstrecke der Kochkurve (4/3)n.
Für n gegen Unendlich geht die Länge der Gesamtstrecke der Kochkurve somit gegen Unendlich.
Die Kochkurve ist eine unendliche Strecke auf einer begrenzten Fläche.
Die Koch-Kurve ist nach ihrer Konstruktionsvorschrift streng selbstähnlich, das heißt, es erscheinen bei beliebiger Vergrößerung immer wieder die gleichen Strukturen.
Die Koch Kurve hat eine Hausdorff-Dimension von
log ( 4 ) / log ( 3 ) ~ 1,26
Kochsche Schneeflockenkurve

Die Koch-Kurve ist auch in Form der "Kochschen Schneeflocke" bekannt, die durch geeignete Kombination dreier Koch-Kurven entsteht.
Als Start wird "F - - F - - F" und als Ersetzungsregel "F -> F + F - - F + F" definiert.
Mit der Ersetzungregel wird die Koch-Kurve generiert.
Die Startregel führ dazu, dass die Kochkurve mit einem Winkel von jeweils 120° aneinandergesetzt wird, so das eine abgeschlossene Kurve entsteht.
Aus dem Start F - - F - - F resultiert ein gleichseitiges Dreieck.