Fraktale - Die Sprache der Natur
"Wolken sind keine Kugeln, Berge keine Kegel, Küstenlinien keine Kreise. Die Rinde ist nicht glatt - und auch der Blitz bahnt sich seinen Weg nicht gerade...
Die Existenz solcher Formen fordert uns zum Studium dessen heraus, was Euklid als formlos beiseite läßt, führt uns zur Morphologie des Amorphen. Bisher sind die Mathematiker jedoch dieser
Herausforderung ausgewichen. Durch die Entwicklung von Theorien, die keine Beziehung mehr zu sichtbaren Dingen aufweisen, haben sie sich von der Natur entfernt. Als Antwort darauf werden wir eine
neue Geometrie der Natur entwickeln und ihren Nutzen auf verschiedenen Gebieten nachweisen.
Diese neue Geometrie beschreibt viele der unregelmäßigen und zersplitterten Formen um uns herum - und zwar mit einer Familie von Figuren, die wir Fraktale nennen
werden."
(Benoit Mandelbrot; 1975, "Die fraktale Geometrie der Natur")
Mit "Fractus" werden zerrissene, unregelmäßig aussehende Wolken der Gattung Cumulus oder Stratus bezeichnet.
Von Natur aus fraktal - Iterierte Funktionssysteme

Fraktale sind überall in der Natur zu finden - wenn man die Natur nur genau betrachtet.
Der Vorteil der fraktalen Geometrie ist, dass mit einer geringen Informationsmenge sehr komplexe und variantenreiche Strukturen definiert werden können.
Fraktale vom Typ IFS (Iterierte Funktionssysteme) werden durch die iterierte Anwendung von Funktionen erstellt, die nach dem Zufallsprinzip ausgewählt werden, wobei immer wieder von einem Ausgangspunkt ausgegangen wird.
Mittels affiner Transformationen kann man z. B. einen Farn auf einfache Weise mathematisch beschreiben:
Xn+1 = aiXn + biYn + ei
Yn+1 = ciXn + diYn + fi
"Barnsley-Farn" und IFS-Fraktal-Baum
Die Matrix des "Barnsley-Farns"
| i | a | b |
c |
d |
e |
f |
p |
| 1 | 0 | 0 | 0 | 0,16 | 0 | 0 | 0,01 |
| 2 | 0,20 | -0,26 | 0,23 | 0,22 | 0 | 1,60 | 0,07 |
| 3 | -0,15 | 0,28 | 0,26 | 0,24 | 0 | 0,44 | 0,07 |
| 4 | 0,85 | 0,04 | -0,04 | 0,85 | 0 | 1,60 | 0,85 |
Die Matrix eines IFS Fraktal-Baums
| i | a | b |
c |
d |
e |
f |
p |
| 1 | 0,200 | -0,500 | 0,340 | 0,400 | 0,440 | 0,250 | 0,200 |
| 2 | 0,460 | 0,410 | -0,250 | 0,360 | 0,250 | 0,570 | 0,200 |
| 3 | -0,060 | -0,070 | 0,450 | -0,110 | 0,600 | 0,097 | 0,200 |
| 4 | -0,350 | 0,070 | -0,470 | -0,020 | 0,490 | 0,500 | 0,200 |
| 5 | -0,640 | 0,000 | 0,000 | 0,500 | 0,860 | 0,250 | 0,200 |
Vorgehensweise zum Zeichnen eines IFS-Fraktals
- Man wähle einen beliebigen Startpunkt (X0 | Y0)
- Wahl der Paramrter nach der entsprechenden Wahrscheinlichkeit
- Berechnung der Abbildung (X1 | Y1)
- Fortführung der Iteration mit dem neuen Punkt (X1 | Y1)
Beispiele für Fraktale in der Natur
Farne, Brokkoli, Wolken, Blutgefäßsysteme, Lunge, Flusssysteme, Blitz, Ammoniten, Dendriten, Bäume...
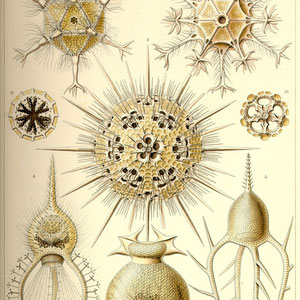
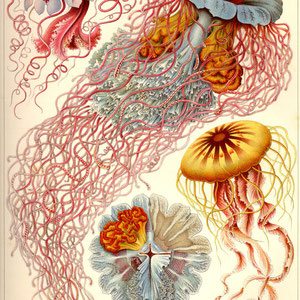
Ernst Haeckel (1834-1919) - Kunst-Formen der Natur
Der Biologe Ernst Haeckel ist berühmt für seine herausragenden Illustrationen seines Buches "Kunstformen der Natur" welches er im Laufe der Jahre 1899-1904 in mehreren Ausgaben
veröffentlichte.
Da das Copyright dieses Werkes von 1904 mittlerweile ausgelaufen ist, möchte ich einzelne Tafeln an dieser Stelle vorstellen, die immer wieder aufs Neue inspirierend sind.
Haeckel hat die biologische Welt und seine Formen in beeindruckender künstlerischer Klarheit und Schönheit dargestellt und somit ganze Generationen von Künstlern beeinflusst.