Selbstähnliche Strukturen

Eine Struktur heißt genau dann selbstähnlich, wenn man die Struktur in Teile zerlegen kann, von denen jedes eine kleine Kopie der Ausgangsstruktur darstellt .

Das Sierpinski-Dreieck entspricht dieser Definition, da jedes der äußeren Dreiecke genügend skaliert wieder kongruent zum Ausgangsdreieck ist.

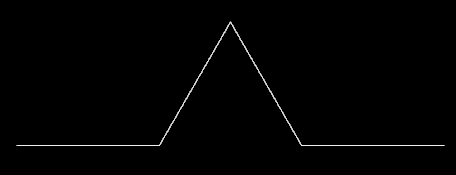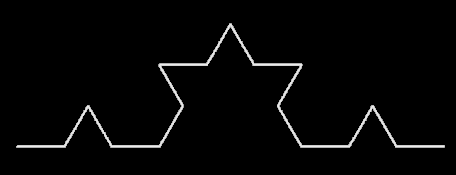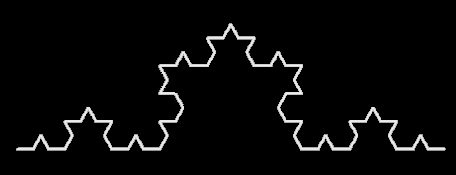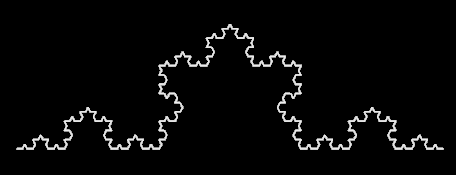
Weitere Beispiel selbstähnlicher Strukturen sind die Cantor-Menge, der Sierpinski-Teppich, die Sierpinski-Pyramide und die Kock-Kurve.

Durch Verwendung fraktaler Strukturen, wie z. B. das Sierpinski-Dreieck oder Koch-Kurven werden in Mobiltelefonen durch Fraktale Antennen eine Erhöhung der Sende- und Empfangsleistung erreicht. Es ist zudem möglich, ein breiteres Spektrum an Frequenzbändern und Funktechnologien abzudecken, ohne dass die Antenne übermäßig groß sein muß oder mehrere Antenne eingebaut werden müssen, was im wahrsten Sinne den Rahmen sprengen würde.